C# - Matrici e sistemi di equazioni lineari

Matrici e sistemi di equazioni lineari

Introduzione

• Una matrice è una tabella ordinata di numeri, organizzata in righe e colonne. Per esempio, la seguente matrice, ha 2 righe e 3 colonne.

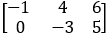
In matematica le matrici sono molto importanti, perché permettono di costruire modelli di sistemi complessi (si vedano testi specializzati per approfondire l’argomento).
Uno degli utilizzi che si prestano maggiormente all’utilizzo delle matrici, è nella risoluzione di sistemi lineari di n equazioni in n incognite. Il metodo che si utilizza è detto “Metodo di Cramer”. Per utilizzare questo metodo è necessario definire il “Determinante” di una matrice e la “Sottomatrice”, poi si potranno applicare le formule di risoluzione.

Determinante di una matrice 2x2

Il determinante di una matrice è un numero che si calcola a partire una matrice quadrata (cioè una matrice che ha tante righe quante colonne). Per le matrici non quadrate, il determinante non ha senso.
Per una matrice 1x1 (cioè fatta da un solo elemento) il determinante è l’elemento stesso.
Data la seguente matrice generica A, quadrata 2x2 (2 righe e 2 colonne):

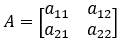
Il determinante si calcola con la semplice formula seguente:

Per esempio, il determinante della matrice:

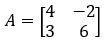
È il seguente:

Determinante di una matrice nxn

Per matrici nxn (con n > 2) la formula del determinante è un po’ più complessa.
Si consideri la generica matrice nxn:

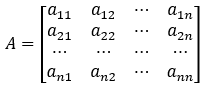
Il determinante di A si può calcolare in vari modi, si riporta qua la formula di Laplace (in due varianti) che si può utilizzare per costruire qualche funzione in C#.

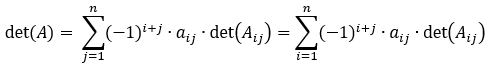
Le due formule precedenti (danno ovviamente lo stesso risultato), in pratica si applicano così:
Si sceglie una riga della matrice (prima formula con la sommatoria sull'indice j) o una colonna della matrice (seconda formula con la sommatoria sull'indice i); conviene scegliere quella che contiene il maggior numero di elementi con 0, perché questo semplifica i calcoli.
Si scorrono tutti gli elementi della riga o della colonna scelta e per ognuno di essi si calcolano i prodotti tra (1) l’elemento stesso e (2) la sottomatrice che si ottiene dalla matrice A rimuovendo la riga i-esima e la colonna j-esima. A questi prodotti si assegna il segno “+” se (i + j) è pari e il segno “-” se (i + j) è dispari. Se l’elemento è nullo, non serve ovviamente calcolare questo prodotto.
Infine, si sommano tutti i prodotti ricavati nel passo precedente.
Per esempio, si calcoli il determinante della matrice:

Si osservi che la quarta riga e la terza colonna hanno due elementi a 0; si sceglie di procedere con la formula di Laplace partendo dalla quarta riga.

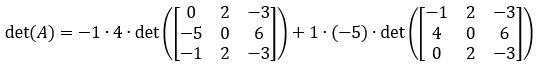
Per le due sottomatrici di ordine 3, si sceglie di procedere con la formula di Laplace partendo rispettivamente dalla prima e dalla seconda riga.

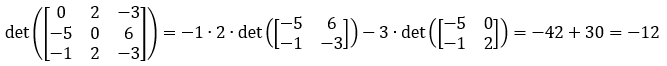
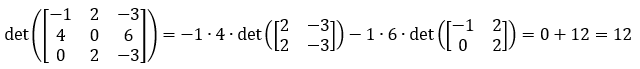
Sostituendo i risultati dei determinanti delle matrici di ordine 3:

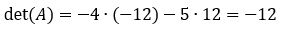
Si noti quindi che il calcolo del determinante di una matrice di ordine ‘n’, passa attraverso il calcolo di determinanti di ordine ‘n-1’. E questo consente di applicare il concetto di ricorsitivà.

Determinante con C#

Le funzioni seguenti, permettono di calcolare il determinante di una matrice nxn. Gli elementi della matrice sono inseriti in un array di ordine n², questo permette una semplificazione nella definizione delle matrici e anche nel codice.
Ecco una funzione per calcolare il determinante di una matrice nxn.

public long Determinant(long[] matrix)

{

// Restituisce il determinante della matrice 'matrix'.

// 'matrix': matrice quadrata, di dimensione almeno 2.

// Per semplicità la matrice è rappresentata da array con gli elementi in fila.

int dim = Convert.ToInt32(Math.Sqrt((double)matrix.Length)); // Dimensione matrice di input.

long ret = 0;

if (dim == 2)

{

ret = matrix[0] * matrix[3] - matrix[1] * matrix[2];

}

else

{

int r = 0; // Riga sulla quale si calcola il determinante.

int k = 0; // +1 o -1, coefficiente.

for (int c = 0; c < dim; c++)

{

if ((r + c) % 2 == 0)

k = 1;

else

k = -1;

ret += k * matrix[r * dim + c] * Determinant(SubMatrix(matrix, r, c));

}

return ret;

}

Si noti che la funzione è ricorsiva, in quanto richiama se stessa, passando come argomento una sottomatrice di ordine inferiore.
Questa funzione necessita del calcolo della sottomatrice, eseguito con la funzione seguente.

public long[] SubMatrix(long[] matrix, int row, int col)

{

// Restituisce la Sottomatrice della matrice 'matrix' eliminando la riga 'row' e la colonna 'col'.

// 'matrix': matrice quadrata, di dimensione almeno 3.

// 'row': indice riga da eliminare, a base 0.

// 'col': indice colonna da eliminare, a base 0.

// Per semplicità le matrici sono rappresentate da array con gli elementi in fila.

int dim = Convert.ToInt32(Math.Sqrt((double)matrix.Length)); // Dimensione matrice di input.

long[] ret = new long[(dim - 1) * (dim - 1)]; // Array di output.

int index = 0;

if (row < 0 || row > (dim - 1))

{

throw new Exception("Row parameter not valid.");

}

if (col < 0 || col > (dim - 1))

{

throw new Exception("Col parameter not valid.");

}

// Ciclo tra tutti gli elementi di matrix.

for (int i = 0; i < dim * dim; i++)

{

// Si eliminano gli elementi della riga 'row'.

if (i < (row * dim) || (i >= (row + 1) * dim))

{

// Si eliminano gli elementi della colonna 'col'.

if (i % dim != col)

{

ret[index] = matrix[i];

index++;

}

return ret;

}

Esempio di utilizzo delle funzioni precedenti:

long det = Determinant(new long[] { 1, 2, 1, 1, 2, 1, 3, 1, 0, 2, 2, 0, 1, 2, 0, 0 });

// Risultato: 10

long det = Determinant(new long[] { -1, 0, 2, -3, 4, -5, 0, 6, 0, -1, 2, -3, 4, -5, 0, 0 });

// Risultato: -12

Sistemi di equazioni lineari

Un sistema di equazioni lineari è un sistema di n equazioni con n incognite:

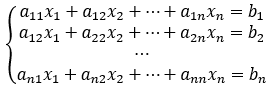
I termini a_ij sono i coefficienti del sistema, b_i sono i termini noti, x_i sono le incognite.
Se le equazioni sono linearmente indipendenti, il sistema ha una unica soluzione (si vedano testi specialistici per la parte teorica).
Dato che il sistema di equazioni ha n equazioni ed n incognite è possibile rappresentare tutti i coefficienti a_ij in una matrice quadrata nxn.
I termini noti b_i e l’insieme delle soluzioni x_i, possono essere invece rappresentati da una matrice costituita da n elementi posti in una sola colonna.
Esistono diversi modi per risolvere un sistema di equazioni lineari; uno di questi è il metodo di Cramer.

Metodo di Cramer

Con il metodo di Cramer, si trovano le soluzioni di un sistema di equazioni lineari.
Le soluzioni sono:

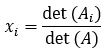
Il denominatore è il determinante della matrice dei termini noti.
Il numeratore è il determinante della matrice ottenuta dalla matrice dei termini noti dopo aver sostituito la colonna i-esima con la colonna dei termini noti.
Per esempio, dato il sistema:

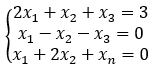
Le matrici dei coefficienti e dei termini noti sono:

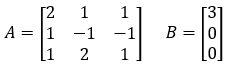
Per calcolare la soluzione, cioè x₁, x₂ e x₃, è necessario calcolare il determinante di A e i tre determinanti ottenuti da A sostituendo rispettivamente la prima, la seconda e la terza colonna con la colonna B.
Quindi (tralasciando un po’ di calcoli):

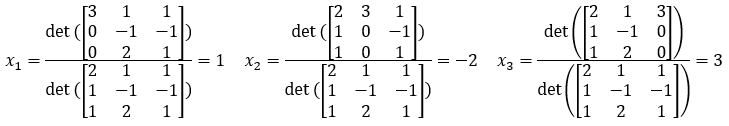
Metodo di Cramer con C#

La funzione seguente risolve, se risolvibile, un sistema lineare di equazioni.

public double[] SolveLinearSystem(long[] matrix, long[] right)

{

// Risolve un sistema lineare di equazioni. Restituisce un vettore con i valori delle incognite.

// 'matrix': matrice quadrata, dei coefficienti.

// 'right': vettore con i termini noti.

// Per semplicità le matrici sono rappresentate da array con gli elementi in fila.

int dim = Convert.ToInt32(Math.Sqrt((double)matrix.Length)); // Dimensione matrice di input.

double[] ret = new double[dim]; // Array di output.

if (right.Length != dim)

{

throw new Exception("Right parameter not valid.");

}

long detA = Determinant(matrix);

if (detA == 0)

{

throw new Exception("Linear System not solvable.");

}

for (int i = 0; i < dim; i++)

{

ret[i] = (double)Determinant(ReplaceMatrixColumn(matrix, i, right)) / (double)detA;

}

return ret;

}

Il sistema non è risolvibile se il determinante di A è nullo e questo succede se le equazioni sono linearmente dipendenti.
La funzione precedente utilizza la funzione ‘Determinant’ precedentemente definita e la funzione ‘ReplaceMatrixColumn’ definita qua sotto:

public long[] ReplaceMatrixColumn(long[] matrix, int col, long[] vector)

{

// Restituisce una nuova matrice dove si sostituisce una colonna con una colonna data.

// 'matrix': matrice quadrata, di dimensione almeno 2.

// 'col': indice colonna da sostituire, a base 0.

// 'vector': array con i dati da inserire.

// Per semplicità le matrici sono rappresentate da array con gli elementi in fila.

int dim = Convert.ToInt32(Math.Sqrt((double)matrix.Length)); // Dimensione matrice di input.

long[] ret = new long[dim * dim]; // Array di output.

if (col < 0 || col > (dim - 1))

{

throw new Exception("Col parameter not valid.");

}

if (vector.Length != dim)

{

throw new Exception("Vector parameter not valid.");

}

// Copia tutti i dati di 'matrix' in una nuova matrice.

for (int i = 0; i < dim * dim; i++)

{

ret[i] = matrix[i];

}

// Sostituzione della colonna.

for (int i = 0; i < dim; i++)

{

ret[col + i * dim] = vector[i];

}

return ret;

}

Esempio di utilizzo delle funzioni:

double[] ret1 = SolveLinearSystem(new long[] { 2, 1, 1, 1, -1, -1, 1, 2, 1 }, new long[] { 3, 0, 0 });

// Risultato: [1, -2, 3]

double[] ret2 = SolveLinearSystem(new long[] { 2, 1, 3, 2, 6, 8, 6, 8, 18 }, new long[] { 1, 3, 5 });

// Risultato: [0.3, 0.4, 0]

double[] ret3 = SolveLinearSystem(new long[] { 1, 2, 1, 4, 2, 0, 4, 3, 4, 2, 2, 1, -3, 1, 3, 2 }, new long[] { 13, 26, 20, 6 });

// Risultato: [2.8(3), -0.3(1), 3.7(6), 1.7(5)]

double[] ret = SolveLinearSystem(new long[] { 1, 1, 1, 4, 2, 1, 9, 3, 1 }, new long[] { 1, 683, 44287 });

// Risultato: [1, -2, 3]