C# - Grafica - L'insieme di Mandelbrot
C#
Le coordinate nelle PictureBox
- Il sistema di coordinate delle PictureBox è il seguente:
- L'origine è l'angolo in alto a sinistra.- La coordinata X va da sinistra a destra.- La coordinata Y va dall'alto verso il basso.
- Rispetto al sistema di coordinate cartesiane, mentre la X coincide, la Y ha il verso opposto.
- È importante considerare anche che le coordinate sono a base 0. Perciò in una PictureBox di 10x10 pixel, si potranno gestire i singoli pixel con la coppia di coordinate X (da 0 a 9) e Y (da 0 a 9).
- Altro fatto da considerare è la proprietà BorderStyle:
- Se BorderStyle = None: la PictureBox non ha il bordo.- Se BorderStyle = FixedSingle: la PictureBox ha un bordo di 1 pixel. Tutti i pixel appartenenti alla cornice esterna di spessore 1, non saranno quindi visualizzati. Una PictureBox di 10x10 pixel avrà un'area visualizzata di 8x8 pixel.- Se BorderStyle = Fixed3D: la PictureBox ha un bordo di 2 pixel. Tutti i pixel appartenenti alla cornice esterna di spessore 2, non saranno quindi visualizzati. Una PictureBox di 10x10 pixel avrà un'area visualizzata di 6x6 pixel.
- Le tre immagini qua sotto, sono gli ingrandimenti di una PictureBox 10x10 pixel (i pixel sono colorati in modo casuale), con i tre BorderStyle impostati rispettivamente a 'None', 'FixedSingle' e 'Fixed3D'.
- Dalle immagini si capisce come l'impostazione del bordo, faccia perdere i pixel delle PictureBox.
- Per gestire la PictureBox con un bordo e senza perderne i pixel sulle coordinate delle cornici, una soluzione è quella di utilizzare un Panel e inserire la PictureBox alle coordinate 0, 0.
- I bordi si possono impostare sul Panel e tutti i pixel della PictureBox saranno visualizzati.
Disegnare in coordinate cartesiane
- Come spiegato nel precedente paragrafo, il sistema di coordinate delle PictureBox (e di tutti gli oggetti) è diverso da quello cartesiano.
- La differenza sta nella coordinata Y che va cambiata di segno ma anche incrementata di una quantità che dipende dall'altezza della PictureBox.
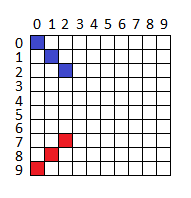
- Per spiegare questo, si consideri la seguente figura.
- La figura rappresenta i pixel di una PictureBox 10x10 pixel. Le coordinate X e Y vanno da 0 a 9. La linea blu, fatta da 3 pixel, è la linea uscente dall'origine con pendenza 45°. La stessa linea nel piano cartesiano è la linea rossa. Non resta che traslare i punti della riga blu, nei punti della riga rossa.
- Sia P1(X1, Y1) il generico punto nel sistema di coordinate della PictureBox.
- Sia P2(X2, Y2) il generico punto nel sistema di coordinate cartesiano.
- Si verifica facilmente:
X2 = X1
Y2 = -Y1 + Ymax
- Dove Ymax è la massima coordinata Y (nella figura sopra Ymax = 9).
Spostare l'origine degli assi
- Le formule del paragrafo precedente sono valide con l'origine degli assi posto nell'angolo alto a sinistra (per il sistema di coordinate della PictureBox). L'origne viene quindi traslato nel sistema di coordinate cartesiane, nell'angolo in basso a sinistra.
- Generalizziamo ora le formule precedenti introducendo l'origine degli assi in qualsiasi punto della PictureBox.
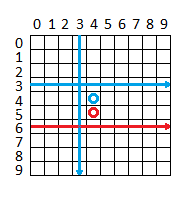
- Si consideri la seguente figura.
- Sia P0(X0, Y0) l'origine degli assi.
- L'origine degli assi della PictureBox (identificato dalle linee azzurre) va spostato traslando l'asse delle ascisse (linea rossa).
- Per esempio, se come in figura, l'origine degli assi è nel punto O(3, 3), l'origine nel sistema cartesiano è il punto O'(6, 3). Il punto P1(1, 1) secondo il sistema PictureBox e disegnato con il pallino azzurro in figura, va spostato nel punto P2(5, 4), disegnato in figura con il pallino rosso.
- In sostanza tutti i punti relativi al sistema cartesiano, hanno coordinate X e Y incrementate rispettivamente di X0 e -Y0. Notare la presenza del segno '-' prima di Y0.
- Riassumendo, le formule di conversione per passare dal sistema di coordinate PictureBox a quello cartesiano, sono:
X2 = X0 + X1
Y2 = - Y0 - Y1 + Ymax
con:
P0(X0, Y0): origine degli assiP1(X1, Y1): punto in coordinate PictureBoxP2(X2, Y2): punto in coordinate cartesiane.
Il piano complesso
- I numeri complessi sono una estensione dei numeri reali.
- Così come i numeri reali si possono rappresentare su una retta, i numeri complessi si possono rappresentare su un piano.
- I numeri complessi sono formati da una coppia di numeri reali. Il primo rappresenta la parte reale del numero, il secondo rappresenta la parte immaginaria.
- Per i numeri complessi valgono le stesse operazioni che ci sono per quelli reali, con qualche accortezza.
- Si rimanda a libri o siti specializzati per ulteriori approfondimenti.
- Esempi di numeri complessi sono:
3 + 2 i --> Parte reale: 3, parte immaginaria: 2- 1 + 4 i --> Parte reale: - 1, parte immaginaria: 48 - 3 i --> Parte reale: 8, parte immaginaria: - 3
- Disegnare sul piano complesso è analogo a disegnare sul piano cartesiano:
- Asse X --> Asse della parte reale- Asse Y --> Asse della parte immaginaria
- Quindi le regole descritte nei paragrafi precedenti sulla rappresentazione nel piano cartesiano, sono le stesse nel piano complesso.
L'insieme di Mandelbrot
[In azzurro, testo tratto da Wikipedia]
- L'insieme di Mandelbrot o frattale di Mandelbrot è uno dei frattali più popolari, conosciuto anche al di fuori dell'ambito matematico per le suggestive immagini multicolori che ne sono state divulgate.
- È l'insieme dei numeri complessi per i quali la successione seguente è limitata:
Z(0) = 0Z(n+1) = z(n)^2 + c
- Nonostante la semplicità della definizione, l'insieme ha una forma complessa il cui contorno è un frattale. Solo con l'avvento del computer è stato possibile visualizzarlo.
- L'insieme prende il nome da Benoît Mandelbrot, colui che nel suo libro Les Objets Fractals: Forme, Hasard et Dimension (1975) rese popolari i frattali.
- In altre parole, si considera il piano complesso e per tutti i punti 'c' di esso, si inizia la successione definita con le formule precedenti.
- Per esempio, considerando il punto c = 1 + i, si ha:
- Z(0) = 0- Z(1) = 1 + i- Z(2) = (1 + i)^2 + (1 + i)
- Man mano che si procede, la successione può divergere o rimanere limitata. Nel secondo caso, il punto iniziale 'c' appartiene all'insieme di Mandelbrot, altrimenti non appartiene.
- Si dimostra che la successione diverge quando il modulo del numero complesso al quale si è arrivati, è maggiore di 2. In tal caso si sospende la successione e si è certi che il punto 'c' non appartiene all'insieme di Mandelbrot.
- Durante la successione si può anche vedere quanto 'velocemente' essa diverge (cioè dopo quante iterazioni il modulo è maggiore di 2). Si può quindi dare una veste artistica a questo insieme, cosa che lo ha reso famoso.
- Per esempio si possono colorare i punti del piano complesso così:
- Nero: il punto appartiene all'insieme di Mandelbrot.- Blu: il punto non appartiene all'insieme di Mandelbrot dopo poche iterazioni.- Sfumature di rosso: il punto non appartiene all'insieme di Mandelbrot dopo molte iterazioni, più il rosso è acceso, più iterazioni ci sono volute.
Disegnare l'insieme di Mandelbrot
- Si vuole fare un programma che mostri l'insieme di Mandelbrot in una PictureBox.
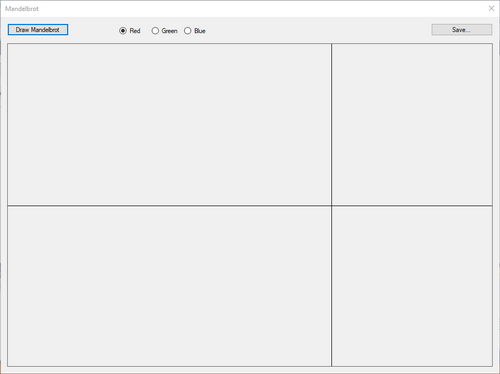
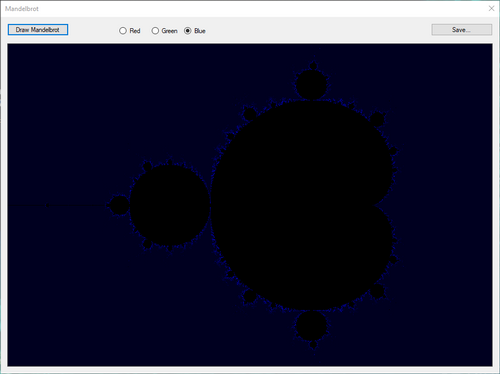
- L'aspetto della form è il seguente:
- Sono presenti i seguenti oggetti:
- La PictureBox "picGraph", dove viene disegnato l'insieme di Mandelbrot (nell'immagine sono anche presenti gli assi del piano complesso). Le dimensioni della PictureBox sono 900x600 pixel. Queste dimensioni sono tali perché l'asse Reale deve essere 1,5 volte l'asse Complesso. L'asse Reale va da -2 a +1, mentre l'asse Complesso da -1 a +1.- Il Bottone "btnDrawMandelbrot", che avvia il disegno.- Il Bottone "btnSave", che permette di salvare il contenuto della PictureBox in un file.- Tre RadioButton "rbRed", "rbGreen" e "rbBlue", che consentono di impostare il colore principale del margine dell'insieme.
- Variabili a livello di Form:
int x0_Center = 600;
int y0_Center = 300;
public struct ColoredPoint
{
public int X;
public int Y;
public Color Color;
}
ColoredPoint[] PictureData = new ColoredPoint[0];
- Il centro, numero complesso (0, 0), è fissato alle coordinate x0_Center e y0_Center che è localizzato nel punto (600, 300) della PictureBox.
- La struct ColoredPoint, contiene le coordinate X e Y di un punto e il colore con il quale deve essere disegnato.
- L'array PictureData è un array di ColoredPoint.
- Il codice del bottone che avvia elaborazione è il seguente:
private void btnDrawMandelbrot_Click(object sender, EventArgs e)
{
LoadPointsOfMandelbrot();
picGraph.Invalidate();
}
- Il primo metodo, LoadPointsOfMandelbrot(), è l'elaborazione vera e propria.
- Il secondo metodo, Invalidate(), invalida la PictureBox permettendone l'aggiornamento.
- Il codice del bottone che salva la PictureBox in un file è il seguente:
private void btnSave_Click(object sender, EventArgs e)
{
SaveFileDialog sfd = new SaveFileDialog();
sfd.Title = "Salva il file"; // Cambia il titolo del form di dialogo.
sfd.Filter = "Bitmap file|*.bmp"; // Imposta le estensioni dei file da filtrare.
sfd.InitialDirectory = Environment.CurrentDirectory; // Imposta la directory iniziale.
sfd.FileName = "mandelbrot.bmp"; // Imposta un nome file di default (l'utente può cambiarlo).
DialogResult res = sfd.ShowDialog();
if (res == DialogResult.OK)
{
string fileName = sfd.FileName; // Directory + nome file.
// Salvataggio del file.
using (var bitmap = new Bitmap(picGraph.Width, picGraph.Height))
{
picGraph.DrawToBitmap(bitmap, picGraph.ClientRectangle);
bitmap.Save(fileName, ImageFormat.Bmp);
}
}
}
- Il salvataggio della PictureBox è fatto su un file bitmap.
- L'evento Paint della PictureBox, viene generato quando la PictureBox viene invalidata.
private void picGraph_Paint(object sender, PaintEventArgs e)
{
DrawAxis(e);
DrawPoints(e);
}
- Il metodo DrawAxis(), disegna le due linee che rappresentano gli assi (Reale e Immaginario) del piano complesso. Le linee vengono poi sovrascritte dall'elaborazione.
- Il metodo DrawPoints(), disegna effettivamente tutti i punti dell'insieme di Mandelbrot.
- Ecco il codice per disegnare gli assi:
private void DrawAxis(PaintEventArgs e)
{
// Costruisce un oggetto Pen impostando il colore nero, spessore 1.
Pen pen = new Pen(Color.Black, 1);
// Disegna l'asse X.
e.Graphics.DrawLine(pen, 0, y0_Center, this.ClientSize.Width, y0_Center);
// Disegna l'asse Y.
e.Graphics.DrawLine(pen, x0_Center, 0, x0_Center, this.ClientSize.Height);
}
- Ed ecco il metodo per disegnare i punti:
private void DrawPoints(PaintEventArgs e)
{
for (int i = 0; i < PictureData.Length; i++)
{
// Disegna il punto, cioè un quadrato di lato 1.
e.Graphics.FillRectangle(new SolidBrush(PictureData[i].Color), PictureData[i].X + x0_Center, -1 * PictureData[i].Y + y0_Center - 1, 1, 1);
}
}
- Come si vede, ogni punto è un elemento dell'array PictureData.
- Per disegnare un unico pixel, occorre disegnare un quadrato di lato 1.
- Infine ecco il metodo che carica l'array PictureData. Questo metodo contiene l'algoritmo di calcolo dell'insieme di Mandelbrot.
private void LoadPointsOfMandelbrot()
{
int MAX_ITERATIONS = 255;
// Una unità sul piano Re / Im è in 300 px.
Array.Resize(ref PictureData, 900 * 600);
int index = 0;
for (int x = -600; x < 300; x++)
{
for (int y = -300; y < 300; y++)
{
Complex c = new Complex(x / 300.0, y / 300.0);
Complex z = c;
for (int iter = 1; iter <= MAX_ITERATIONS; iter++)
{
// Se modulo è > 2, la serie sicuramente diverge: non appartiene all'insieme.
if (z.Magnitude > 2.0)
{
// In base al numero di iterazioni per divergere, si assegna un colore.
PictureData[index].X = x;
PictureData[index].Y = y;
if (iter <= 32)
iter = 32;
if (iter > 255)
iter = 255;
if (rbRed.Checked)
PictureData[index].Color = Color.FromArgb(iter, 0, 0);
else if (rbGreen.Checked)
PictureData[index].Color = Color.FromArgb(0, iter, 0);
else // if (rbBlue.Checked)
PictureData[index].Color = Color.FromArgb(0, 0, iter);
// Prossimo punto.
break;
}
// Se ultima iterazione, la serie non diverge: appartiene all'insieme.
if (iter >= MAX_ITERATIONS)
{
PictureData[index].X = x;
PictureData[index].Y = y;
PictureData[index].Color = Color.Black;
// Prossimo punto.
break;
}
// Iterazione.
z = Complex.Add(Complex.Multiply(z, z), c);
}
index++;
}
}
}
- I cicli for, permettono di iterare tra tutti i pixel del piano complesso.
- Il terzo ciclo for, è l'iterazione di Mandelbrot, fatta al massimo 255 volte.
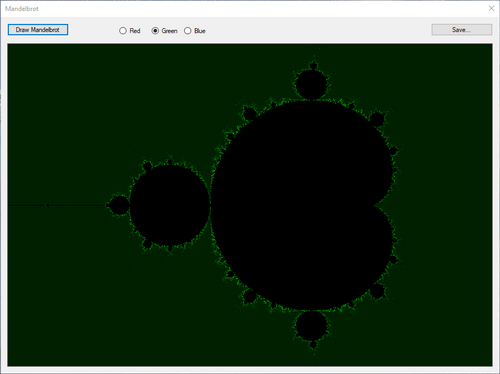
- Al pixel viene assegnato il colore nero se dopo 255 iterazioni non diverge. Altrimenti viene assegnato una sfumatura di colore (rosso, verde o blu) in base al numero di iterazioni che ha impiegato l'algoritmo a divergere.
- Il risultato che si ottiene è il seguente, in base al colore selezionato: