Crittografia a chiave pubblica

DOCS

Crittografia a chiave pubblica

Introduzione

Obiettivo: Si vuole inviare un messaggio da A a B in modo sicuro. Nel canale di trasmissione si può introdurre chiunque e leggere i dati trasmessi.
Il messaggio da spedire non può essere in chiaro (come una cartolina) perché chiunque potrebbe leggerlo.
Il messaggio va quindi criptato. Questo è facile se A e B riescono a mettersi d’accordo sul modo in cui criptare il messaggio, per esempio possono decidere un metodo e una chiave di codifica.

Il problema è che spesso A e B non si conoscono. In questo caso la crittografia a chiave pubblica risolve il problema. L’interlocutore sarà in grado di decodificare il messaggio. Invece tutti gli anelli della catena di comunicazione, anche vedendo lo stesso messaggio, non saranno in grado di farlo.

Un segreto condiviso

Un qualsiasi messaggio di testo può essere trasformato in sequenze di numeri. Per esempio basta far corrispondere ogni carattere con il suo codice ASCII. La trattazione seguente perciò tratterà numeri.
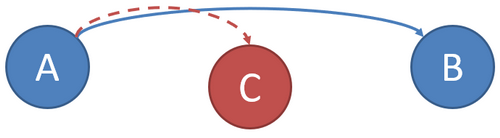
Riassumendo, A vuole trasmettere a B un numero, C può intercettare tutti i messaggi, ma non deve capire il numero.
Esempio, A vuole comunicare a B il numero segreto 123.
A non può dire 123 direttamente, altrimenti C che intercetta tutti i messaggi, capisce.
Supponiamo che A e B abbiano una informazione «condivisa» cioè che conoscono entrambi, per esempio il numero 555. E questa informazione non è nota a C.
A calcola la somma tra il numero segreto e l’informazione condivisa: 123 + 555 = 678.
Allora A trasmette il messaggio: «Il numero è 678 meno il numero condiviso».
B può decodificare il messaggio facendo 678 – 555 = 123.
C non può ricavare il numero originale, perché non conosce il numero 555.
Osservazioni:

Il segreto «condiviso» nella realtà sarà molto più complesso di un numero di sole 3 cifre, altrimenti C proverà tutte le combinazioni per decodificare il messaggio.
Chiamiamo le cose col giusto nome. Il segreto condiviso è detto da ora in poi «chiave» ed è lungo 128 o 256 bit. (Trasformato in cifre è come un numero di rispettivamente circa 38 o 76 cifre).
Nel mondo reale la chiave non verrà semplicemente sommata al messaggio, ma messaggio e chiave saranno elaborati a blocchi in modo più o meno complessi in modo da resistere ad attacchi di tipo statistico.
Dobbiamo stabilire la chiave; se A e B si conoscono, si mettono d’accordo sulla chiave, ma nel mondo reale quando si fa un acquisto in Internet per esempio, nessun Cliente si mette d’accordo con alcun Sito sulla chiave da utilizzare. E qua entrano in gioco le chiavi pubbliche e private. (Scambio di chiavi Diffie-Hellman da Whitfield Diffie e Martin Hellman)

Quindi: l’obiettivo diventa stabilire una chiave tra A e B senza che essi si mettano d’accordo segretamente e senza che C possa ricavarla durante la trasmissione di messaggi tra A e B.

Esempio semplificato

Nelle righe seguenti è descritto il metodo per creare una chiave condivisa tra A e B, senza che C la scopra o la deduca.
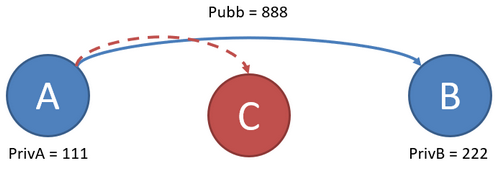
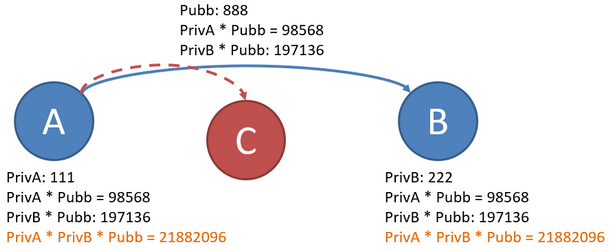
A e B generano autonomamente un numero segreto «la chiave privata» che custodiscono gelosamente. Esempio: A genera 111 e B genera 222.
Uno solo tra A e B (è lo stesso) genera un numero che viene diffuso ed è detto «chiave pubblica». Esempio: 888.
La chiave pubblica è visibile da tutti, compreso C.

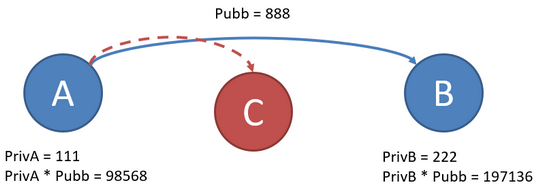
Sia A che B generano due nuove chiavi moltiplicando la propria chiave privata con quella pubblica.
A: 111 * 888 = 98568
B: 222 * 888 = 197136

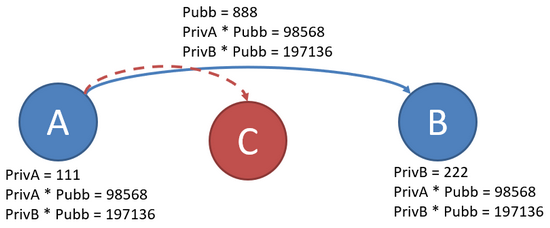
Ora A e B si scambiano le nuove chiavi. Poiché utilizzano un canale di trasmissione, chiunque può leggerle.

Infine sia A che B generano la nuova chiave moltiplicando la propria chiave privata alla chiave ricevuta dall’altro.
A: PrivA * (PrivB * Pubb) = 111 * 197136 = 21882096
B: PrivB * (PrivA * Pubb) = 222 * 98568 = 21882096

Siamo arrivati alla fine.
A e B hanno calcolato autonomamente il numero 21882096. A non conosce la chiave privata di B e B non conosce quella di A.
C conosce la chiave pubblica, ha intercettato le chiavi private sommate alla pubblica, ma non può ricavare al numero 21882096.
Quindi: abbiamo raggiunto l’obiettivo, che era stabilire una chiave tra A e B
senza che essi si mettano d’accordo segretamente e senza che C possa ricavarla durante la trasmissione di messaggi tra A e B
.

Ritorno alla realtà

L’esempio numerico, utilizza la «moltiplicazione» per ricavare le nuove chiavi. Non possiamo utilizzarlo nella realtà, perché la moltiplicazione è una operazione invertibile (con la «divisione») e B potrebbe ottenere la chiave privata di A semplicemente dividendo la chiave ottenuta da A (PrivA * Pubb) con la chiave pubblica. E viceversa A potrebbe ottenere la chiave privata di B.
Occorre quindi utilizzare una operazione «non invertibile» che dati due numeri ne ottenga un terzo e che non sia invertibile (cioè dato il risultato e uno dei due numeri non permetta di ottenere l’altro numero).
Quale operazione matematica non invertibile possiamo utilizzare?
Ci vengono in aiuto due concetti:

La matematica modulare (il nome sembra difficile, in realtà si ragiona con il concetto di «resto» della divisione).
La classica elevazione a potenza.

Esempio di matematica modulare

Se per esempio si lavora con «modulo 11», le operazioni restituiscono un risultato compreso tra 0 e 10 che è il resto della divisione con 11.
456 = 41 * 11 con resto 5 --> si scrive --> 456 % 11 = 5
Si legge: «Il resto della divisione di 456 con 11 è 5» oppure «456 modulo 11 è 5».

La crittografia reale

Ecco di seguito tutto il processo precedente utilizzando la matematica modulare.

A e B scelgono una chiave privata

Esempio con numeri piccoli per poterne seguire i calcoli.
PrivA = 15
PrivB = 22

A o B sceglie due numeri da utilizzare per creare la chiave pubblica

Diversamente dall'esempio semplificato, la chiave pubblica è "generata" a partire da due numeri.
Il primo è il «modulo» (per esempio 11) e il simbolo è %.
Il secondo è la «base» (per esempio 3).

A e B creano il numero «PubblicoPrivato»

Non si fa più la moltiplicazione (che abbiamo visto è invertibile) ma si fa questa operazione (si indica con il simbolo ^ l'elevazione a potenza):
PubbPrivA = base^PrivA % modulo --> PubbPrivA = 3^15 % 11 = 1
PubbPrivB = base^PrivB % modulo --> PubbPrivB = 3^22 % 11 = 9

A e B scambiano i numeri «PubblicoPrivato»

Questi due numeri sono i numeri che vengono scambiati tra A e B (e potenzialmente intercettabili da chiunque).

A e B creano la «chiave»

KeyA = PubbPrivB^PrivA % modulo --> 9^15 % 11 = 1
KeyB = PubbPrivA^PrivB % modulo --> 1^22 % 11 = 1

Quindi:

A e B hanno ottenuto la stessa chiave utilizzando:

la propria chiave privata e
un mix tra la chiave pubblica e la chiave privata dell’altro.

Il fatto che KeyA = KeyB = Key (cioè che le due chiavi siano identiche) non è molto complesso da dimostrare. Infatti si eleva la base due volte con gli stessi due esponenti, ma in ordine inverso.
C osserva le due chiavi pubbliche («modulo» e «base») e anche le due chiavi PubbPrivA e PubbPrivB e con questi numeri non è in grado di risalire alla chiave Key.
Anche A non è in grado di risalire alla PrivB e viceversa B non è in grado di risalire a PrivA.

Le chiavi pubbliche nella realtà sono molto più grandi. Infatti la Key ottenuta è un numero compreso tra 0 e il «modulo» – 1. Se si sceglie come modulo 11, con solo 11 tentativi (tra 0 e 10) si decodificherebbe il messaggio. Nella pratica si sceglie un numero di centinaia di cifre.
Qualche altro accorgimento.

Nel calcolare le potenze della «base», se non la si sceglie accuratamente, il modulo (rispetto a un certo valore) delle potenze potrebbe ciclare tra pochi valori e non tra tutti i possibili.

In pratica:

Si sceglie come «modulo» un numero primo.
Si sceglie come «base» una radice primitiva del modulo (cioè la base può assumere determinati valori, qua la matematica può essere complessa).

Ogni volta che si va in un sito Web sicuro (https), in pratica computer e server si scambiano la Key con il metodo Diffie-Hellman (o una variante).
Ci sono altri metodi? Certo, senza scambio di chiavi, ma utilizzando la chiave pubblica. Per esempio RSA (da Ronald Rivest, Adi Shamir e Leonard Adleman) (vedi lo scambio di certificati e le vecchie chiavette delle banche).