C# - Algoritmi sui grafi 2
C#
L'algoritmo di Djkstra
Introduzione
- L'algoritmo di Dijkstra si applica a un grafo e permette di calcolare il cammino minimo da un nodo a tutti gli altri nodi e ne indica il percorso. I pesi dei nodi sono orientati e non devono essere negativi.
- Ogni nodo in questo algoritmo ha le seguenti proprietà:
- Distanza attuale.
- Flag: Definitivo (true / false se la distanza trovata è quella definitiva).
- Nodo Predecessore.
- I passi dell’algoritmo sono i seguenti.
- Inizializzare il nodo di partenza con Distanza = 0, Definitivo = false, Predecessore = ‘’.
- Inizializzare tutti gli altri nodi con Distanza = infinita, Definitivo = false, Predecessore = ‘’.
- Finché ci sono nodi non definitivi:
- Selezionare il nodo con Distanza minore (quindi si inizia con il nodo di partenza).
- Impostare per questo nodo il valore Definitivo = true.
- Aggiornare la Distanza dei nodi collegati a questo nodo selezionato (e che non siano definitivi). Essa va impostata al minimo tra la Distanza attuale del nodo collegato e la Distanza che avrebbe il nodo collegato passando per il nodo selezionato. Se la Distanza viene aggiornata, impostare come Predecessore il nodo selezionato.
Esempio
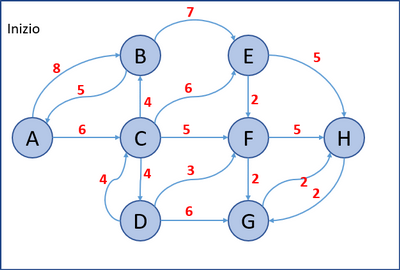
- In questo esempio si applica l’algoritmo di Dijkstra per trovare le minime distanze tra il nodo A e gli altri nodi del grafo seguente:
- Inizializzazione del grafo:
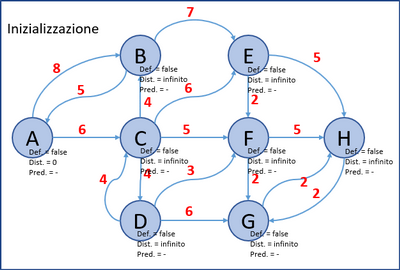
- Si seleziona il nodo con la distanza minore: A. Si aggiornano (se necessario) i nodi non definitivi ad esso collegati: B e C.
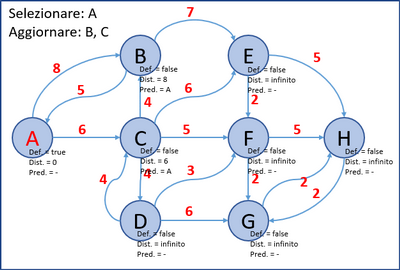
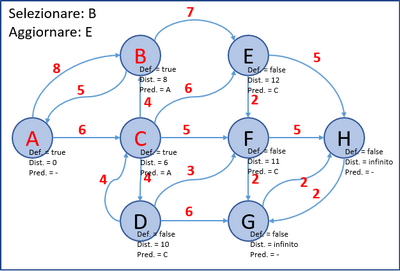
- Allo stesso modo, si selezionano nell’ordine i nodi: C, B, D, F, E, G e H e si aggiornano (se necessario) i nodi non definitivi ad essi collegati.
- Nelle immagini seguenti, viene mostrata l'evoluzione dell'algoritmo.

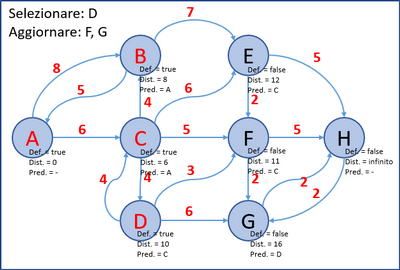
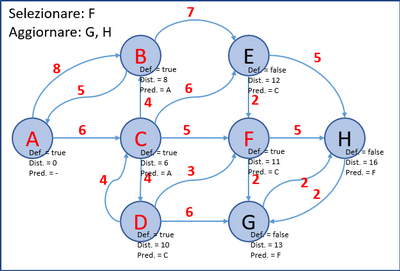
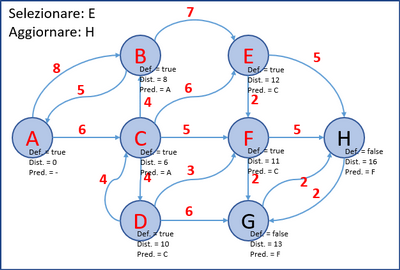
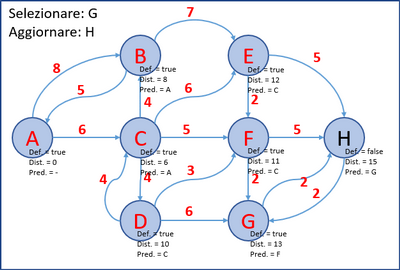
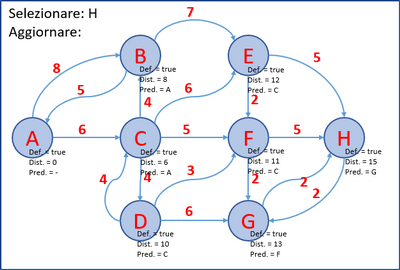
- L’ultimo grafo è il grafo finale; in ogni nodo è presente la distanza minima dal nodo A e il nodo predecessore.
- Per esempio, il cammino minimo tra A e H è: A, C, F, G, H.
L'algoritmo in C#
- Il codice seguente, utilizza le seguenti due classi che definiscono gli oggetti 'Nodo' e 'Collegamento tra due nodi'.
// Descrive i nodi del grafo: ogni oggetto è un nodo.
public class DijkstraNode
{
public int Node { get; set; }
public int Distance { get; set; }
public bool Definitive { get; set; }
public int Predecessor { get; set; }
}
// Descrive i collegamenti tra i nodi del grafo: ogni oggetto è un collegamento tra Node1 e Node2.
public class DijkstraEdge
{
public DijkstraNode Node1 { get; set; }
public DijkstraNode Node2 { get; set; }
public int Distance { get; set; }
}
- Con il codice seguente, si inizializza una lista con i nodi e una con i collegamenti. Essi sono relativi all'esempio del paragrafo precedente.
// Preparazione e inizializzazione lista dei nodi.
List<DijkstraNode> lstNodes = new List<DijkstraNode>();
for (int i = 0; i <= 7; i++)
{
lstNodes.Add(new DijkstraNode() { Node = i, Distance = Int32.MaxValue, Definitive = false, Predecessor = -1 });
}
// Preparazione lista degli archi.
List<DijkstraEdge> lstEdges = new List<DijkstraEdge>();
lstEdges.Add(new DijkstraEdge() { Node1 = lstNodes[0], Node2 = lstNodes[1], Distance = 8 });
lstEdges.Add(new DijkstraEdge() { Node1 = lstNodes[0], Node2 = lstNodes[2], Distance = 6 });
lstEdges.Add(new DijkstraEdge() { Node1 = lstNodes[1], Node2 = lstNodes[0], Distance = 5 });
lstEdges.Add(new DijkstraEdge() { Node1 = lstNodes[1], Node2 = lstNodes[4], Distance = 7 });
lstEdges.Add(new DijkstraEdge() { Node1 = lstNodes[2], Node2 = lstNodes[1], Distance = 4 });
lstEdges.Add(new DijkstraEdge() { Node1 = lstNodes[2], Node2 = lstNodes[3], Distance = 4 });
lstEdges.Add(new DijkstraEdge() { Node1 = lstNodes[2], Node2 = lstNodes[4], Distance = 6 });
lstEdges.Add(new DijkstraEdge() { Node1 = lstNodes[2], Node2 = lstNodes[5], Distance = 5 });
lstEdges.Add(new DijkstraEdge() { Node1 = lstNodes[3], Node2 = lstNodes[2], Distance = 4 });
lstEdges.Add(new DijkstraEdge() { Node1 = lstNodes[3], Node2 = lstNodes[5], Distance = 3 });
lstEdges.Add(new DijkstraEdge() { Node1 = lstNodes[3], Node2 = lstNodes[6], Distance = 6 });
lstEdges.Add(new DijkstraEdge() { Node1 = lstNodes[4], Node2 = lstNodes[5], Distance = 2 });
lstEdges.Add(new DijkstraEdge() { Node1 = lstNodes[4], Node2 = lstNodes[7], Distance = 5 });
lstEdges.Add(new DijkstraEdge() { Node1 = lstNodes[5], Node2 = lstNodes[6], Distance = 2 });
lstEdges.Add(new DijkstraEdge() { Node1 = lstNodes[5], Node2 = lstNodes[7], Distance = 5 });
lstEdges.Add(new DijkstraEdge() { Node1 = lstNodes[6], Node2 = lstNodes[7], Distance = 2 });
lstEdges.Add(new DijkstraEdge() { Node1 = lstNodes[7], Node2 = lstNodes[6], Distance = 2 });
// Esegue l'algoritmo.
Dijkstra(lstEdges, lstNodes);
// Stampa il risultato.
foreach (var node in lstNodes)
{
Console.WriteLine(String.Format("Node: {0} Definitive: {1} Distance: {2} Predecessor: {3}", node.Node, node.Definitive, node.Distance, node.Predecessor));
}
- Infine, ecco il codice dell'algoritmo vero e proprio.
private void Dijkstra(List<DijkstraEdge> lstEdges, List<DijkstraNode> lstNodes)
{
// Inizializza il nodo di partenza: il primo della lista.
lstNodes[0].Distance = 0;
// Finché ci sono nodi non definitivi...
while (lstNodes.Where(p => !p.Definitive).Count() != 0)
{
// Seleziona il nodo con distanza inferiore.
var node = lstNodes.Where(p => !p.Definitive).OrderBy(p => p.Distance).FirstOrDefault();
if (node != null)
{
// Questo nodo diventa definitivo.
node.Definitive = true;
// Ricerca di tutti i nodi collegati al nodo selezionato, non definitivi.
List<DijkstraNode> linkedNodes = lstEdges.Where(p => p.Node1.Node == node.Node).Select(p => p.Node2).Where(p => p.Definitive == false).ToList();
// Per tutti i nodi collegati:
foreach (var linkedNode in linkedNodes)
{
// Calcolo della distanza tra il nodo iniziale e 'linkedNode', passando per 'node'.
int distanza = node.Distance + lstEdges.Where(p => p.Node1 == node && p.Node2 == linkedNode).First().Distance;
// Se la distanza appena calcolata è migliore della distanza attuale:
if (distanza < linkedNode.Distance)
{
// Si aggiorna il 'linkedNode'.
linkedNode.Distance = distanza;
linkedNode.Predecessor = node.Node;
}
}
}
else
{
break;
}
}
}
